Panduan Sederhana untuk Rasio Poisson dan Modulus Young

Materials can talk to us. They tell us how they will act when we put pressure on them. They let us know how much they can pull, bend, and get squeezed before they break. They speak using the ideas of mechanics and numbers. Two of the most important ideas are Young’s Modulus dan Poisson’s Ratio. If you want to know how we build things and why they stay in one piece, you have to know about these two ideas. In this post, I will explain this in a simple way. You will learn what these properties are. You will see why they are important. And you will understand how we use them to make our world safer.

What Is Young’s Modulus, and Why Is It So Important for an Engineer?

Let me tell you about Young’s Modulus. You can think of it as how stiff a material is. It is a number that shows how much a material fights back when you pull it or squeeze it. Let’s say you have a spring made of steel and a spring made of plastic. The steel spring is much harder to pull. Do you know why? It’s because steel has a much bigger Young’s Modulus than plastic. It is a material with more rigidity. This one property is very, very important for an engineer. We need it when we design anything, from a big building to a small paperclip.

Another name for this property is the modulus of elasticity. We find its value using a unit called Pascals. But the numbers are very big, so we often use Gigapascals, or GPa. Steel can have a Young’s Modulus of 200 GPa. Rubber might have one of 0.01 GPa. That big difference tells an engineer what material to use for a job. If I need something that won’t bend when a loading is on it, I need a material with a high Young’s Modulus. This mechanical property is a key part of choosing materials. It is a basic parameter for all structural design and a big part of the mechanics of materials.

How Do We Find Out How Stiff a Material Is?

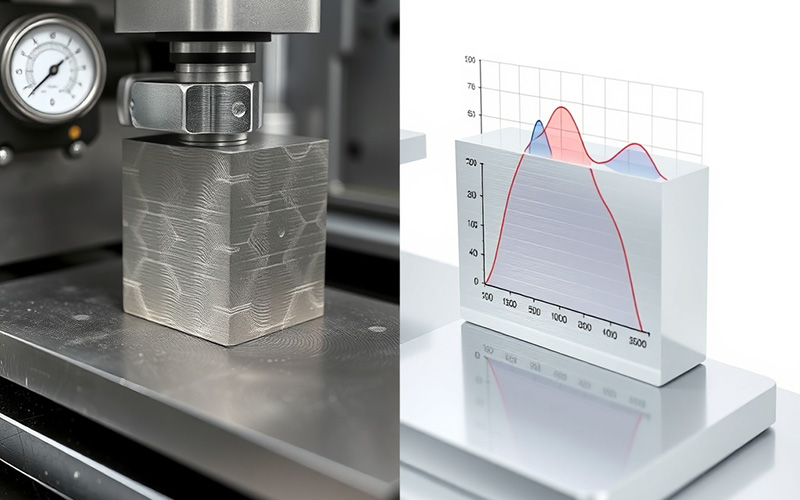
So, how do we get this useful number? We find it by doing a test. The test we use most often is the tensile test. We take a sample of the material. It is often in the shape of a dog bone. We put it into a machine. The machine pulls it from its two ends. The machine writes down the applied load, which is the force used to pull. It also writes down the strain, which is how much the sample gets longer. This experimental test lets us measure how a material acts under loading. The specimen will deform, or change shape, because of the tensile force.

From this test, we make a graph. The graph is called a stress-strain curve. Stress is the force we apply over the area of the sample. Strain is the change in the length. For most materials, the start of this curve is a straight line. This part is the “elastic” area. This means the material will go back to its old shape if you stop pulling. Young’s Modulus is just the slope, or the steepness, of this straight line. A very steep slope means a high Young’s Modulus and a lot of stiffness. A line that is not steep means the opposite. We can also use a tangent to the curve to find the modulus. This measurement is a very basic part of testing materials.

What Is Poisson’s Ratio and How Does It Explain Material Behavior?

Now, let’s talk about the second important idea in our story. This idea is Poisson’s Ratio. This one is a bit different. It does not tell us about stiffness. Instead of that, it tells us about the shape of a material. Think about pulling a rubber band. You know it gets longer. But did you ever see that it also gets thinner? Poisson’s Ratio is the number that talks about this effect. It is a ratio that looks at the strain on the sides compared to the strain in the direction you are pulling.

To be exact, it is the ratio of the transverse strain to the axial strain. The transverse strain is how much it gets thinner. The axial strain is how much it gets longer. Since one side gets smaller as the other gets bigger, the ratio is a positive number. This property is a ratio with no units. That means it is just a number. For most materials, this number is between 0 and 0.5. A ratio of 0.5 means the material cannot be squeezed into a smaller space. Its total bulk size stays the same when you pull on it. This parameter is another one of the main elastic properties we need to understand a material. A famous mathematician from France came up with the idea for this ratio.

Did You Ever Pull a Rubber Band? A Simple Way to See Poisson’s Ratio.

I used to pull rubber bands as far as they could go. I could see them get very long and also very thin. I did not know it at the time, but I was doing a simple experimental test of Poisson’s Ratio. Rubber has a Poisson’s Ratio that is close to 0.5. This high ratio means it gets a lot thinner when you pull on it. This is easy to see. It helps to demonstrate this important property.

Now, let’s think about a piece of metal, like steel or aluminum. If you pull on a metal rod, it will also get thinner. But the change is very small. It is much too small for your eyes to see. A normal metal has a Poisson’s Ratio of about 0.3. This lower ratio tells us that the thinning effect is not as big. This ratio that shows much a material thins when pulled is a key part of its mechanical behavior. It is one of the elastic moduli that helps tell the full story about a material. This simple ratio is a very useful tool.

Are Young’s Modulus and Poisson’s Ratio Connected? A Look at the Correlation.

This is a question that I am asked a lot. Do these two numbers relate to each other? The short answer is no, not in a simple way. For most materials, Young’s Modulus and Poisson’s Ratio are seen as separate elastic properties. This means you cannot find one just by knowing the other one. A material can be very stiff, with a high Young’s Modulus. It can also have a high or a low Poisson’s Ratio. There is no easy mathematical rule that connects them for every material.

But, there is a correlation, or a connection, between them. This happens when we look at the whole picture of a material’s elasticity. For materials that are homogeneous and isotropic, these two values are part of a bigger family of elastic moduli. A homogeneous and isotropic material has the same properties in every direction. You only need to know two of these elastic moduli to find all of the others. So, if you measure Young’s Modulus dan Poisson’s Ratio, you can find other important properties. These include the shear moduli or the bulk modulus. This is how the two values relate in a roundabout way. They work together to paint a full picture.

What Is the Interplay Between All the Elastic Properties?

Let’s look a little more at this family of properties. The way they work together is a key idea in materials science. We have four main elastic moduli. They describe the elasticity of a homogeneous and isotropic material:

1. Young’s Modulus (E): How it fights being pulled (tensile) or squeezed (compressive).
2. Poisson’s Ratio (ν): The ratio of getting thin to getting long.
3. Shear Modulus (G): Also known as the modulus of rigidity. It measures how it fights being twisted.
4. Bulk Modulus (K): How it fights being squeezed from every side (a change in its volumetric size).

These four are all connected to each other. They relate through easy mathematical equations. As an example, the shear moduli can be worked out if you know Modulus Young dan Rasio Poisson. This tells us that these properties do not exist by themselves. They are all different ways to talk about the same basic material’s elastic properties. This is a very basic idea in solid mechanics. Knowing how they work together lets an engineer fully estimate how a material will act.

Here is a simple table. It shows how Modulus Young dan Rasio Poisson berbeda:

How Do Experimental Tests in Materials Science Give Us Answers?

In materials science, we cannot just make a guess for these numbers. We have to measure them. We do this with experimental tests. As I said before, the tensile test is the classic way to get the stress-strain curve and to find Modulus Young. We can also use it to measure the change in the diameter of the sample. This helps us find Rasio Poisson. But there are other, newer ways to do this.

A new way is the indentation test. In this experimental test, we push a very hard and small tip into the top of a sample. The tip is often made of diamond. We measure how much force is needed to make a small dent. From this, we can estimate the material’s elastic properties. This includes Modulus Young. Another way is to use sound wave propagation. We send a fast sound wave through the material. Then we measure how quickly it moves. The speed of this wave has a direct link to the elastic moduli. These experimental tests are very important. They give us the right numbers we need to build things. You can read many papers about these tests on websites like ScienceDirect.

Can This Special Ratio Be a Negative Number? A Look at Odd Materials.

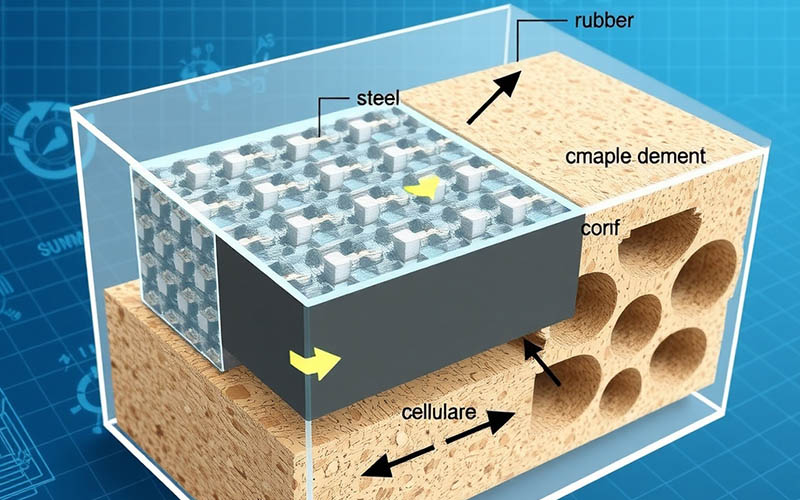
Here is something fun to know. I said that Poisson’s Ratio is most of the time between 0 and 0.5. But some very strange, special materials actually have a negative Poisson’s Ratio. What does this mean? It means that when you pull on them, they get lebih tebal! These materials are called auxetic materials. They are not very common. But they have very interesting mechanical properties. Think about a bandage that gets tighter on a cut when you bend your arm. That is something we might be able to do with them.

These materials often have a very special inside structure, or microstructure. It might be like a special honeycomb or foam. This microstructure is made to deform in this strange way. This is a great way to show how materials science can make materials with a property not seen in nature. The ratio of these materials is a really interesting thing to study. They demonstrate how we can build material behavior on a tiny level to get great results on a bulk level. This is where an engineer can be creative and implement new ideas.

Why Are These Two Properties So Basic in Mechanics?

For a structural engineer, Modulus Young dan Rasio Poisson are not just numbers on a page. They are basic tools. When I design a part for a machine, I must know how it will deform when there is loading on it. Will it bend too much? Will its shape change in a way that makes other parts break? Modulus Young helps me estimate the bending and pulling. Poisson’s Ratio helps me know about the change in shape in all 3D directions.

Without these two constant values, engineering would be like guessing. We could not build safe planes, bridges that last a long time, or medical parts we can trust. We utilize these properties in computer programs. These programs can guess how a part will act before we even make it. This saves us time and money. Even more important, it helps keep people safe. These numbers are the base of today’s mechanical design and engineering. A defect in knowing these elastic properties can cause a defect in the thing we build.

Let’s Put It All Together: A Real-World Example for an Engineer.

Let’s think about this. You are an engineer. You have to pick a metal to make a bolt. This bolt will have tensile loading on it. The first thing you worry about is that the bolt does not stretch too much. So, you look for a material with a high Young’s Modulus. Steel is a great pick. Its high Young’s Modulus means it has high rigidity and will not stretch much. This property is the main parameter you look at.

But then you have to think about the whole thing. The bolt fits into a hole. If the bolt gets too thin when you make it tight, it might get loose. Or it might not make a good seal. This is where you have to think about the Poisson’s Ratio. You need to work out how much the bolt’s diameter will get smaller with the applied load. You use the ratio to do this math. Most of the time, the change is small. But in various engineering jobs that need to be very exact, even a tiny change is important. This shows how Poisson’s Ratio and Young’s Modulus work with each other. They give us the full story. One tells you about the change in length. The other tells you about the change in width. An engineer has to think about both of them.

Things to Remember

• Modulus Young is about stiffness. A big value means the material is very stiff. It is hard to pull.
• Rasio Poisson is about shape. It is a ratio. It tells you much a material gets thinner when you pull on it.
• These two properties are usually separate from each other. But they are both parts of a family of elastic moduli. Together, they describe a material’s elasticity.
• We measure these values with experimental tests. These tests include the tensile test or an indentation test.
• For any engineer who builds things, these two mechanical properties are very basic. They help us know how a material will act under loading. They are the special language of materials.