Deixe a Istar ajudá-lo a iniciar o seu projeto com a nossa experiência e know-how!
Carregue os seus ficheiros de desenho e requisitos de produção e entraremos em contacto consigo no prazo de 30 minutos!

Você já pensou por que um elástico volta ao lugar, mas um clipe de papel permanece dobrado? Ou por que algumas coisas esticam muito antes de quebrar, enquanto outras quebram imediatamente? Eu costumava pensar nessas perguntas também. Bem, existe um gráfico especial que nos mostra exatamente como as coisas agem quando você as puxa. Chama-se curva de tensão-deformação e é uma das ideias mais importantes da mecânica dos materiais.
Este artigo será seu mapa. Veremos o que é uma curva de tensão-deformação. Aprenderemos a lê-la. E veremos o que ela nos diz sobre objetos do cotidiano. Você descobrirá por que os engenheiros acham essas curvas de tensão-deformação tão úteis. Eles as usam para construir de tudo, desde pontes até aviões. Ao final, você poderá olhar para um gráfico simples e aprender sobre os pontos fortes e fracos secretos escondidos dentro do material.
Para obter a curva de tensão-deformação, primeiro precisamos conhecer suas duas partes principais. Essas partes são tensão e deformação. Elas podem parecer difíceis, mas são realmente simples. Imagine-se em uma disputa de cabo de guerra com uma corda. A força que você está usando na corda cria uma força dentro dela. Essa força é chamada de tensão. Para ser exato, tensão é definida como a quantidade de força aplicada a algo, espalhada por sua área. Pense nisso como quanta "pressão" o material sente por dentro. Portanto, uma força maior na mesma corda significa mais tensão.
Agora, o que está acontecendo com a corda enquanto você a puxa? Ela está esticando! Esse esticamento é chamado de deformação. Deformação nos diz o quanto algo muda sua forma por causa da tensão. Se a corda fica um pouco mais longa, ela tem um pouco de deformação. Se ela estica muito, ela tem muita deformação. Então, você pode pensar em tensão e deformação como uma equipe. Uma causa a outra. Você aplica tensão (a força) e obtém deformação (o esticamento).
Se você entender como tensão e deformação trabalham juntas, você pode entender muito sobre um material. Esse trabalho em equipe é exatamente o que a curva de tensão-deformação nos mostra. Quando puxamos algo, chamamos de tensão de tração. Quando esmagamos algo, chamamos de tensão de compressão. Para nosso mapa, falaremos principalmente sobre puxar coisas.
Então, como as pessoas fazem esses gráficos úteis? Eles usam uma máquina especial para fazer um teste de tração. Imagine que você pega um pedaço de um material. Ele geralmente tem o formato de um osso de cachorro. Você o coloca em uma máquina de teste. Esta máquina tem grampos fortes que seguram cada extremidade do material. Então, a máquina de teste começa lentamente a puxar o material. Este é um puxão uniaxial. Isso significa apenas que ele puxa em uma única linha reta.
À medida que a máquina de teste puxa com mais e mais força à temperatura ambiente, ela mede duas coisas ao mesmo tempo:
A máquina coloca esses pontos em um gráfico. Ela coloca a tensão subindo e descendo, e a deformação indo de um lado para o outro. A linha que é desenhada é a famosa curva de tensão-deformação! Apenas um teste nos dá toneladas de informações. Ele nos diz tudo sobre as propriedades mecânicas daquele pedaço de materiais de engenharia.
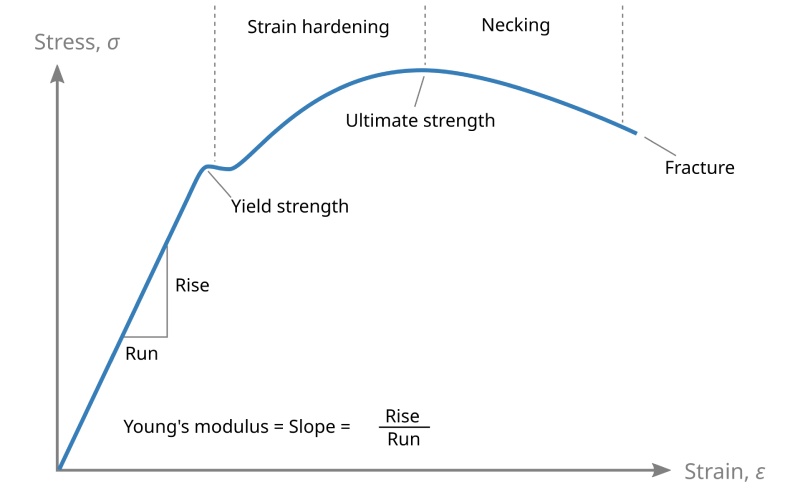
Quando você olha pela primeira vez para uma curva de tensão-deformação típica para um metal, você verá que a curva começa com uma linha que é perfeitamente reta. Ela sobe e para a direita. Chamamos esta parte reta de área elástica linear. O que isso significa? Significa que o material age como um elástico novo. Quando você o puxa, ele estica. Quando você o solta, ele volta à sua forma original. Chamamos isso de ação elástica. O material não foi alterado para sempre.
Nesta parte da curva, a tensão é proporcional à deformação. Esta é uma regra famosa na ciência. Se você tornar a tensão duas vezes maior, você torna a deformação duas vezes maior. Este trabalho em equipe perfeito continua até chegar a um ponto especial. Este ponto é chamado de limite proporcional. A linha é completamente reta até este ponto proporcional. É uma parte muito simples da história. Ela mostra os primeiros sinais de elasticidade do material. Esta linha reta é chamada de porção linear da curva.
Esta porção da curva é muito importante para os engenheiros. Eles querem fazer coisas que permaneçam dentro do limite elástico. Isso é para coisas que usamos todos os dias. Por exemplo, você não quer que uma ponte permaneça torta depois que um caminhão passa por ela! O limite proporcional é o ponto onde a relação tensão-deformação deixa de ser uma linha reta. Logo depois disso está o limite elástico. Este é o último ponto onde o material pode voltar à sua forma original quando você o solta.
A primeira parte da curva de tensão-deformação é uma linha reta. Toda linha reta tem uma inclinação. Essa inclinação tem um nome especial. É chamado de Módulo de Elasticidade. Às vezes é chamado de Módulo de Young. Eu sei, isso soa chique. Mas é apenas um número. Ele nos diz o quão rígido um material é. Um material rígido, como o aço, terá uma inclinação muito íngreme. Isso significa que você precisa de muita tensão para obter apenas um pouco de deformação.
Pense nisso desta forma: é muito difícil esticar uma barra de aço. Isso porque seu módulo de elasticidade é um número muito grande. Por outro lado, um material como a borracha tem uma inclinação que não é muito íngreme em sua curva de deformação. Você não precisa de muita tensão para obter muita deformação. É por isso que a borracha é tão elástica! Então, o módulo é apenas a tensão dividida pela deformação naquela área elástica. O módulo de elasticidade é uma propriedade chave. Ele ajuda os engenheiros a escolher o material certo para um trabalho.
| Material | Rigidez (Módulo) | Aparência e Sensação |
|---|---|---|
| Aço | Muito elevado | Uma régua de metal rígida |
| Alumínio | Elevado | Uma lata de refrigerante |
| Plástico | Baixa | Uma garrafa de água de plástico |
| Borracha | Muito baixo | Um elástico |
Encontramos este número, o módulo, descobrindo a inclinação da parte reta e linear da curva. É uma maneira muito importante de medir a elasticidade do material.
Se continuarmos a puxar nosso material além do limite elástico, algo diferente acontece. A curva de tensão-deformação não é mais reta. Ela começa a dobrar. Este é o ponto chamado de ponto de escoamento. O ponto de escoamento é um ponto chave em nosso gráfico. Este é o ponto onde o material deixa de ser elástico. Ele começa a mudar para sempre. Chamamos isso de deformação plástica.
Pense em dobrar um clipe de papel. Você pode dobrá-lo um pouco e ele voltará à sua forma (isso é elástico). Mas se você dobrá-lo demais, ele permanece dobrado. Você ultrapassou seu ponto de escoamento. Você está agora na área de deformação plástica. A quantidade de tensão que você precisa para chegar a este ponto é chamada de resistência ao escoamento ou tensão de escoamento. Uma vez que você ultrapassa a resistência ao escoamento, o material terá uma deformação permanente. Isso acontece mesmo depois que você para de puxar. Você o mudou para sempre!
Para algumas coisas, como o aço macio, o ponto de escoamento é muito fácil de ver. A curva pode até mesmo descer um pouco. Isso significa que o material de repente começa a esticar muito. Você nem precisa adicionar muita força. Isso acontece porque partes muito pequenas dentro do metal começam a se mover. Este é o início de uma deformação permanente. Induzir deformação plástica significa apenas que você tem que usar tensão suficiente para ultrapassar este ponto.
Esta é uma parte muito interessante da história. Depois que o material começa a mudar para sempre (passado a tensão de escoamento), você pode pensar que ele está apenas ficando mais fraco. Mas para muitos materiais, como um metal, a curva de tensão-deformação começa a subir novamente! Isso significa que o material está realmente ficando mais forte à medida que muda de forma. Esta característica legal é chamada de encruamento.
Então, o que está acontecendo dentro? À medida que o material é esticado, todos os pequenos pedaços dentro ficam misturados e emaranhados. Este emaranhado torna mais difícil para eles se moverem. Então, você precisa aplicar mais e mais tensão para mantê-lo esticando. Chamamos esta parte do gráfico de região de encruamento. O material fica mais resistente. Isso acontece devido ao encruamento.
Você já dobrou um arame para frente e para trás? Você provavelmente viu que fica mais difícil dobrar cada vez. Isso é encruamento em ação! Você está tornando o metal mais forte, mas também o está tornando menos elástico. É assim que o material luta contra mais mudanças. É aqui que a deformação ocorre. A tensão aumenta à medida que a deformação aumenta nesta área.
À medida que continuamos a puxar e o material continua a ficar mais duro, a curva de tensão-deformação continua a subir. Ela finalmente chega a um pico. Este é o ponto mais alto em toda a curva. Este pico é chamado de resistência à tração máxima (UTS). Esta é a maior quantidade de tensão de engenharia que o material pode suportar. Depois deste ponto, ele começa a ficar mais fraco.
A resistência à tração máxima é um número muito importante. Ela diz a você a maior força de tração que um material pode suportar. Se você usar uma tensão que é maior do que a UTS, o material vai quebrar. É o rei da colina na curva de tensão-deformação. Qualquer valor de tensão passado este ponto significa que o material em breve quebrará.
Você pode pensar nisso como o último grande momento do material. Ele esticou. Ele ficou mais duro através do encruamento. E agora está em seu ponto mais forte. Deste ponto em diante, as coisas começam a descer. Isso leva à quebra final, que é chamada de fratura. A tensão máxima é uma informação muito importante. Os engenheiros precisam dela para projetar peças fortes.
Depois de chegar ao ponto mais alto, a resistência à tração máxima, algo estranho começa a acontecer. A curva de tensão-deformação começa a apontar para baixo. Mas espere, como a tensão pode diminuir enquanto ainda estamos puxando? Isso é por causa de algo que chamamos de estricção.
Quando o material está perto de quebrar, um pequeno ponto começa a ficar fino. Parece que um pescoço está se formando. A área da seção transversal no pescoço fica menor. Porque é menor, não pode suportar tanta força. A força está agora toda naquela pequena área. Então a tensão real dentro do pescoço ainda está subindo! Chamamos isso de tensão verdadeira. Mas a máquina está medindo a força com base na primeiro área da seção transversal. Então a tensão que ela calcula parece diminuir. Esta é a tensão de engenharia.
Esta região de estricção mostra que o material não é mais estável. Todo o esticamento agora acontece naquela pequena área do pescoço. A estricção começa logo após a UTS ser alcançada. O processo de estricção continua. A seção transversal fica cada vez menor. Então, o material finalmente quebra.

O fim da curva de tensão-deformação é o ponto de fratura. É aqui que o material finalmente se quebra em duas partes. Para um material dúctil, como muitos metais, esta fratura acontece após muito esticamento e muita estricção. Se você olhar para as peças quebradas de um material dúctil, você frequentemente verá uma forma chamada de fratura "copo e cone". Um lado parece um copo e o outro parece um cone. Este é um sinal claro deste tipo de quebra.
Toda a área sob a curva de tensão-deformação nos diz sobre a tenacidade do material. Tenacidade é uma maneira de medir quanta energia algo pode absorver antes de quebrar. Algo com uma alta resistência à tração máxima que também estica muito é muito tenaz. Sua curva terá uma grande área sob ela. Ela pode lidar com muita energia antes de quebrar. Esta é uma característica muito boa para muitos trabalhos.
A jornada que vemos na curva de tensão-deformação, desde o primeiro esticamento elástico até a fratura final, nos dá uma imagem completa das propriedades de um material. Ela nos diz sua força, sua rigidez e quão bem ela pode absorver energia. A área sob a curva de tensão-deformação mostra a quantidade de energia de deformação que é absorvida por unidade de volume.
Nem todas as curvas de tensão-deformação parecem iguais. Realmente, a forma da curva é como uma impressão digital para um material. Ela diz a você se o material é dúctil ou frágil. Como vimos, um material dúctil (como aço ou cobre) tem uma longa curva de tensão-deformação. Ele estica muito. Ele também mostra um ponto de escoamento claro, encruamento e estricção antes de quebrar.
Mas materiais frágeis (como vidro ou cerâmica) têm um tipo muito diferente de curva de tensão-deformação. Sua curva é muito curta e íngreme. Um material frágil mostra quase zero deformação plástica. Ele estica um pouco na área elástica e então simplesmente quebra! Não há aviso. Não há ponto de escoamento. E não há estricção. É por isso que um vidro se estilhaça imediatamente quando você o deixa cair.
Então, um engenheiro pode olhar para a forma de uma curva de tensão-deformação e saber muito sobre como esse material vai agir. Para o caso de materiais dúcteis, a quebra é lenta. Mas materiais frágeis têm uma quebra que é rápida e repentina. A curva de tensão-deformação original conta toda a história. Podemos também olhar para a tensão verdadeira e a deformação verdadeira. Isso nos dá uma imagem melhor, especialmente na região de estricção. Ela corrige os números para a área da seção transversal em mudança. A deformação de engenharia e a deformação normal são maneiras mais fáceis de medir. Elas usam o comprimento inicial.