Let Istar help you get started on your project with our experience and know-how!
Upload your design files and production requirements and we will get back to you within 30 minutes!

When I was new to building things, the name “Young’s Modulus” seemed hard to understand. But, a teacher showed me an easy way to see it. I want to share that with you today. This guide will show you how to figure out Young’s modulus. We will use simple examples and an easy math problem. You will find out what this important trait tells us about a material. This article is for anyone who wants to know how different materials act. It is for students, people who make things, and anyone who is curious.
I see Young’s Modulus as a way to measure how stiff something is. It tells you how much a material will stretch or bend when you push or pull on it. Think about pulling on a rubber band and a steel rod. The rubber band stretches with no problem. The steel rod hardly moves at all. This happens because the steel material has a very high Young’s modulus. The rubber material has a low Young’s modulus. People also call this trait the modulus of elasticity or elastic modulus. It is a main mechanical trait of any solid material.
This modulus is a number. A larger number means the material is more stiff. A smaller number means the material is more bendy. This idea is a very important part of building things and the study of materials. We need this modulus to make safe bridges and strong parts. Each material has its own modulus of elasticity. Knowing this trait of a material helps us pick the right one for a job. The modulus helps us guess how a material will act when a force is used on it. This special trait does not change for a certain material.
To get what Young’s modulus is, we first have to learn about stress and strain. I learned that stress is the force you apply on a material. Then you divide that force by the material’s cross-sectional area. You can picture it as how much force is pushing or pulling on a very small spot of the material. We measure stress using units of pressure. A common unit is Pascals (Pa). The math problem for stress (σ) is:
Strain tells us how much the material changes shape because of the stress. It is the change in its length, and you divide that by the first length of the material. Strain does not have any units. This is because it is a comparison of two lengths. A material with a lot of strain changes its shape a lot. The math problem for strain (ε) is:
These two ideas, stress and strain, are connected. In most materials, when you use small forces, stress and strain change together in a steady way. This means if you make the stress two times bigger, you make the strain two times bigger. This connection is the secret to finding the modulus. The way stress and strain are connected is a very basic trait of any material. The modulus of elasticity helps us explain this mechanical action.
The math problem to figure out Young’s modulus is easy after you learn about stress and strain. I always think of it as “stress over strain.” Young’s Modulus (E) is the stress put on the material divided by the strain that happens. This easy math problem tells us a great deal about the material. It only works in the material’s elastic region. This is where the material goes back to its first shape after the force is taken away.
Here is the main math problem to get the modulus:
Young’s Modulus (E) = Stress (σ) / Strain (ε)
We can write this math problem in a longer way using the formulas for stress and strain:
E = (F / A) / (ΔL / L₀)
Where:
This math problem is a very helpful tool. With only a few things to measure, we can figure out a very important trait of a material. This work is a normal job when building things. Using a calculator can make this work go very fast. The answer is the Young’s modulus, a number that tells us about the material’s stiffness.
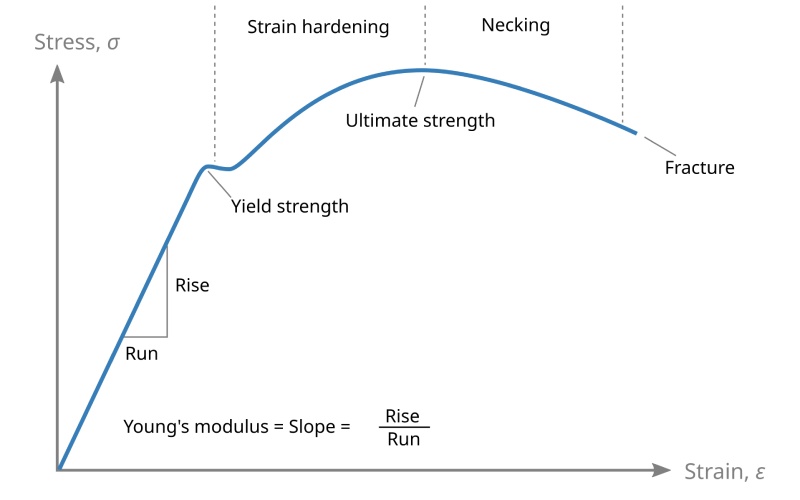
A stress-strain curve is a graph. It shows you how a material acts when you put a force on it. I have used these curves many times to learn about a new material. The stress is on the y-axis, which is the line that goes up and down. The strain is on the x-axis, which is the line that goes side to side. When you first put a force on it, the graph is a straight line. This is the linear elastic region. The material acts like a spring in this part.
The steepness of this straight line on the curve is the Young’s modulus. A line that goes up sharply means a higher modulus, so the material is more stiff. A line that goes up slowly means a lower modulus, and the material is more bendy. This straight-line part is where the stress and strain change together steadily. If you take away the force in this area, the material goes back to its first length. This graph gives us a picture of the material’s mechanical trait.
After the straight-line part, the curve might start to bend. This is where the material starts to change shape for good. This is known as plastic deformation. The stress-strain curve is a very useful tool for learning about any material. Different materials like metals and plastics have curves that look very different. Looking at the curve tells us a lot about the material’s strength and how it acts. The modulus is found only from the first, straight part of the graph.
To figure out Young’s modulus, you have to measure a few things. I recall doing this in a science room. First, you need a piece of the material. It is often in the form of a rod or a thin wire. You will also need a way to put a force that you know on this piece of material. This is usually done with weights.
Here is a list of tools you might use to measure and get the modulus:
Measuring the cross-sectional area is very important to get the right answer. You put on a force, then you measure how much the length changed. You do this again for a few different forces. With this information, you can figure out stress and strain for each force. Then you can make the graph or use the math problem to find the modulus of the material. This set of steps helps us find a key mechanical trait of the material.
Let’s do an example of the math together. Let’s pretend we have a steel rod. This is a material used a lot in building things. I’ll use some sample numbers to make it simple to see. A calculator will be a big help with the math.
Let’s say our steel rod has:
First, let’s figure out the stress: Stress (σ) = F / A = 10,000 N / 0.0001 m² = 100,000,000 Pa
Next, we figure out the strain: Strain (ε) = ΔL / L₀ = 0.001 m / 2 m = 0.0005
Last, we figure out Young’s modulus: Young’s Modulus (E) = Stress / Strain = 100,000,000 Pa / 0.0005 = 200,000,000,000 Pa
This number is 200 GigaPascals (GPa). This is the known Young’s modulus for steel. This work shows how we can find the stiffness of this one kind of material. The way to figure out the modulus is the same for any material that is elastic.
The modulus of elasticity is not the same for every material. This is because of how it is made on the inside. I like to think of it this way: the small atoms in a material are held together by connections. In a stiff material like steel, these connections are very strong. It takes a great deal of force to pull them apart. This means it has a high modulus. In a material that bends easily like rubber, the connections are not as strong and can stretch more. This gives rubber a low modulus of elasticity.
The table below shows the Young’s modulus for a few common materials. You can see how much they are not alike. This difference is a big deal when making and building things.
| Material | Young’s Modulus (GPa) |
|---|---|
| Rubber | 0.01-0.1 |
| Aluminum | 69 |
| Steel | 200 |
| Diamond | 1220 |
This trait of a material comes from what its atoms are like. The way atoms are set up and linked tells us the material’s stiffness. This is why a light material like aluminum has a lower modulus than a heavy material like steel. The modulus of a material is a very basic mechanical trait that we cannot change easily. We have to pick the material that has the right modulus for what we need.
From what I have seen, the modulus of a material is one of the biggest things to think about when you build something. When we make a plan for something, we need to guess how it will act when different forces are on it. The modulus lets us do that. For instance, when making a bridge, builders must pick a material with a high modulus of elasticity, like steel. This makes sure the bridge will not bend too much from the weight of cars.
A material with a high modulus gives stiffness and strength. For an airplane wing, builders might pick a material like aluminum or a mix of materials. These materials have a good mix of stiffness (a high enough modulus) and are not heavy. Picking the material and its modulus is a very important part of the planning work. A wrong choice of material could cause it to break. We use the modulus to figure out shape changes and to be sure a building is safe. This science idea has a very big effect on our everyday lives. The modulus of the material decides how it can be used.

The linear elastic area is the part of the stress-strain curve where you can tell what will happen. When you put a force on a material in this area, the shape change is elastic. “Elastic” means that when you take the force away, the material goes back to its first shape and length. Think of pulling a spring just a tiny bit. It goes right back. This is an elastic shape change. The material’s action is linear. This means stress and strain have a simple, direct connection.
This is the area where our math problem for Young’s modulus works just right. The connection where stress and strain change together steadily is known as Hooke’s Law. The modulus is the number that shows what this connection is. For any plan where we do not want lasting bending or breaking, we make sure the forces on the material keep it inside this elastic area. Knowing about this area is the key to using a material in a safe way. This trait is very important.
Until now, I have mostly talked about pulling a material, which is named tension. But we can also push on a material, which is named compression. Young’s modulus is for both of these. It measures the material’s stiffness when a force is put on it from end to end. For most materials, like steel or concrete, the Young’s modulus in tension and compression is the same.
When you use a pushing force, the material becomes shorter. The stress is a pushing stress, and the strain is a pushing strain. The math to get the modulus is the same: stress divided by strain. The only thing that is different is that the change in length is a negative number. So, it does not matter if you pull an object or push it. The modulus of elasticity tells you how the material will fight that change. This one modulus number gives us a lot of information about how the material acts under both kinds of force.